将数列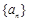
中的所有项按每一行比上一行多两项的规则排成如下数表：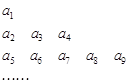
已知表中的第一列数
构成一个等差数列, 记为
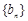, 且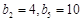
, 表中每一行正中间一个数
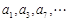构成数列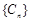
, 其前n项和为
.
(1)求数列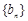的通项公式；(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且
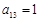.①求；②记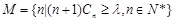
, 若集合M的元素个数为3, 求实数
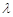的取值范围.
相关试题
，倾斜角为
的直线
过椭圆的左焦点
，与椭圆
交于
两点，若以
为直径的圆过椭圆的右焦点
，求
的值.
的两个焦点分别为
，离心率为
.
的方程；
分别为
，求线段
的中点
的轨迹方程，并说明轨迹是什么曲线.
底面
，其中
，
平面
锥
的体积
的余弦值（理科）相关知识点
推荐套卷
将数列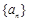中的所有项按每一行比上一行多两项的规则排成如下数表：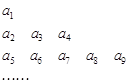
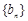已知表中的第一列数构成一个等差数列, 记为, 且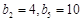, 表中每一行正中间一个数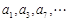构成数列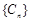, 其前n项和为.
(1)求数列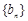的通项公式；(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且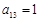.①求；②记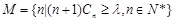, 若集合M的元素个数为3, 求实数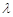的取值范围.
粤公网安备 44130202000953号