如图1,在一个不透明的袋子中装有四个球,分别标有字母A、B、C、D,这些球除了字母外完全相同,此外,有一面白色、另一面黑色、大小相同的四张正方形卡片,每张卡片两面的字母相同,分别标有字母A、B、C、D。最初,摆成如图2的样子,A、D是黑色,B、C是白色.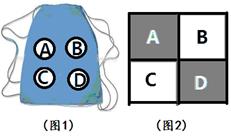

两次操作后观察卡片的颜色。
(如:第一次取出A、第二次取出B,此时卡片的颜色变成 )
)
(1)取四张卡片变成相同颜色的概率;
(2)求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率.
相关知识点
推荐套卷
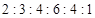 .第三组的频数是12.请你回答:
.第三组的频数是12.请你回答:
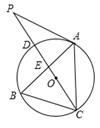

 的过顶抛物线是F2,四边形ABCD的面积为
的过顶抛物线是F2,四边形ABCD的面积为 ,请直接写出点B的坐标.
,请直接写出点B的坐标. ,如果PD=1,∠BPD=90°,请直接写出点A到BP的距离.
,如果PD=1,∠BPD=90°,请直接写出点A到BP的距离.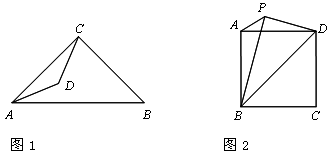
 经过点A(4,0)和B(0,2).
经过点A(4,0)和B(0,2).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号