如图1，在△ABC中，CA=CB，∠ACB=90°，D是△ABC内部一点，∠ADC=135°，将线段CD绕点C逆时针旋转90°得到线段CE，连接DE．
（1）①依题意补全图形；
②请判断∠ADC和∠CDE之间的数量关系，并直接写出答案．
（2）在（1）的条件下，连接BE，过点C作CM⊥DE，请判断线段CM，AE和BE之间的数量关系，并说明理由．
（3）如图2，在正方形ABCD中，AB=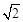
，如果PD=1，∠BPD=90°，请直接写出点A到BP的距离．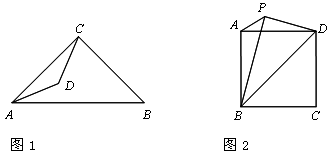
相关试题
等腰Rt△ABC中，∠BAC=90°，点A、点B分别是x轴、y轴两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E。
（1）如图（1），若A(0，1)，B(2，0)，求C点的坐标；
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB=∠CDE；
（3）如图（3），在等腰Rt△ABC不断运动的过程中，若满足BD始终是∠ABC的平分线，试探究：线段OA、OD、BD三者之间是否存在某一固定的数量关系，并说明理由。
相关知识点
推荐套卷
粤公网安备 44130202000953号