为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:
| A.10本以下; | B.10~15本; | C.16~20本; | D.20本以上.根据统计整理并制作了如图所示的两幅统计图表: |
(1)在这次调查中一共抽查了 名学生;
(2)表中x,y的值分别为:x= ,y= ;
(3)在扇形统计图中,C部分所对应的扇形的圆心角是 度;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.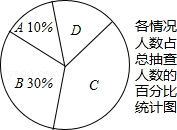

相关知识点
推荐套卷
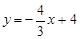 与
与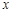 轴交于点
轴交于点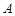 ,与
,与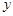 轴交于点
轴交于点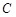 ,已知二次函数的图象经过点
,已知二次函数的图象经过点 .
.
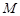 ,求四边形
,求四边形 的面积;
的面积;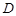 、
、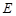 同时从点
同时从点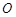 出发,其中点
出发,其中点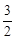 个单位长度的速度沿折线
个单位长度的速度沿折线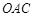 按
按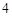 个单位长度的速度沿折线
个单位长度的速度沿折线 按
按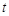 秒时,
秒时,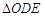 的面积为S .
的面积为S . ∥
∥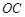 ,若存在,请求出此时
,若存在,请求出此时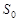 是②中函数S的最大值,那么
是②中函数S的最大值,那么 与抛物线
与抛物线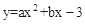 交于A,B两点,点A在x轴上,点B的纵坐标为3。点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
交于A,B两点,点A在x轴上,点B的纵坐标为3。点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D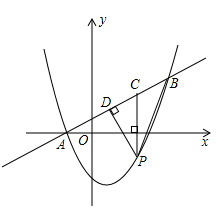
 的值
的值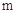
 的对称轴为
的对称轴为 )
) 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
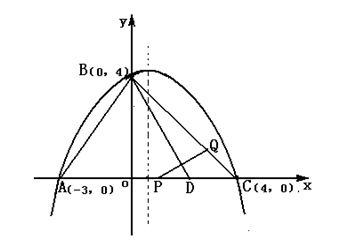
 中,直线
中,直线 交x轴于A点,交y轴于B点,过A、B两点的抛物线
交x轴于A点,交y轴于B点,过A、B两点的抛物线 交
交 轴于另一点C,点D是抛物线的顶点.
轴于另一点C,点D是抛物线的顶点.
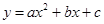 上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等? 若存在,请求出此时点M的坐标,若不存在,请说明理由.
上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等? 若存在,请求出此时点M的坐标,若不存在,请说明理由. 
 粤公网安备 44130202000953号
粤公网安备 44130202000953号