如图：抛物线经过A（-3，0）、B（0，4）、C（4，0）三点.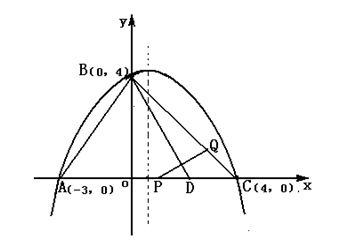

（1）求抛物线的解析式.
（2）已知AD = AB（D在线段AC上），有一动点P从点A沿线段AC以每秒1个单位长度的速度移动；同时另一个动点Q以某一速度从点B沿线段BC移动，经过t 秒的移动，线段PQ被BD垂直平分，求t的值；
（3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ+MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由。
（注：抛物线的对称轴为）