在无穷数列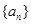 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
, . 设
. 设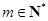 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.
(1)设数列 为1,3,5,7,
为1,3,5,7,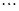 ,写出
,写出 ,
, ,
,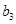 的值;
的值;
(2)若 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列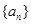 ;
;
(3)设 ,
,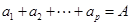 ,求
,求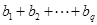 的值.(用
的值.(用 表示)
表示)
推荐套卷
在无穷数列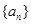 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
, . 设
. 设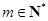 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.
(1)设数列 为1,3,5,7,
为1,3,5,7,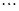 ,写出
,写出 ,
, ,
,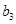 的值;
的值;
(2)若 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列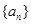 ;
;
(3)设 ,
,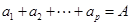 ,求
,求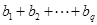 的值.(用
的值.(用 表示)
表示)