将等腰Rt△ABC和等腰Rt△ADE按图1方式放置，∠A=90°， AD边与AB边重合， AB＝2AD＝4．将△ADE绕点A逆时针方向旋转一个角度α（0°≤α≤180°），BD的延长线交直线CE于点P.
（1）如图2，BD与CE的数量关系是 , 位置关系是 ；
（2）在旋转的过程中，当AD⊥BD时，求出CP的长；
（3）在此旋转过程中，求点P运动的路线长.[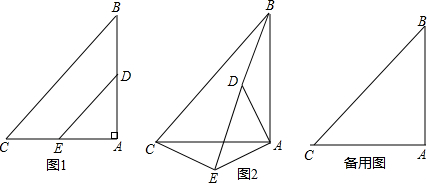
的解是负数．求k的取值范围.
再选择一个你喜欢的值代入求值
推荐套卷
将等腰Rt△ABC和等腰Rt△ADE按图1方式放置，∠A=90°， AD边与AB边重合， AB＝2AD＝4．将△ADE绕点A逆时针方向旋转一个角度α（0°≤α≤180°），BD的延长线交直线CE于点P.
（1）如图2，BD与CE的数量关系是 , 位置关系是 ；
（2）在旋转的过程中，当AD⊥BD时，求出CP的长；
（3）在此旋转过程中，求点P运动的路线长.[
粤公网安备 44130202000953号