一个口袋中装有大小形状完全相同的红色球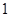 个、黄色球
个、黄色球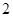 个、蓝色球
个、蓝色球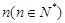 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得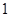 分、摸到黄球得
分、摸到黄球得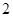 分、摸到蓝球得
分、摸到蓝球得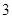 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出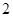 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是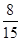 .
.
⑴求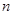 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出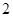 个球,设
个球,设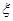 表示所摸
表示所摸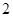 球的得分之和,求
球的得分之和,求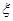 的分布列和数学期望
的分布列和数学期望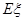 .
.
推荐套卷
一个口袋中装有大小形状完全相同的红色球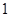 个、黄色球
个、黄色球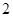 个、蓝色球
个、蓝色球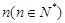 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得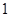 分、摸到黄球得
分、摸到黄球得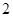 分、摸到蓝球得
分、摸到蓝球得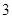 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出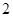 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是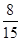 .
.
⑴求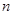 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出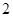 个球,设
个球,设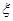 表示所摸
表示所摸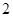 球的得分之和,求
球的得分之和,求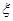 的分布列和数学期望
的分布列和数学期望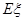 .
.