某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组[13, 14)；第二组[14, 15)，……，第五组[17, 18]. 下图是按上述分组方法得到的频率分布直方图.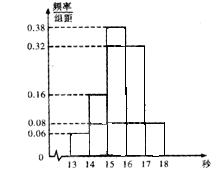
(1)若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
(2)设m、n表示该班某两位同学的百米测试成绩，且已知m, n∈[13, 14)∪[17, 18]. 求事件“|m－n|>1”的概率.
相关试题
cosx(x∈R)．
设数列{an}共有n（
）项，且
，对每个i (1≤i≤
，i
N)，均有
．
（1）当
时，写出满足条件的所有数列{an}（不必写出过程）；
（2）当
时，求满足条件的数列{an}的个数．
，点E是棱AB上一点．且
．
；
，求
的值．
R．
．相关知识点
推荐套卷
粤公网安备 44130202000953号