如图，正三角形ABC的边长为2，D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠，使A、B、C三点重合，构成三棱锥A— DEF ．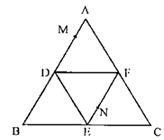
(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上，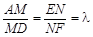
(λ＞O，λ为变量)
①当λ为何值时，MN为异面直线AD与EF的公垂线段? 请证明你的结论②设异面直线MN与AE所成的角为a，异面直线MN与DF所成的角为β，试求a+β 的值
＋
＋
的最大值．
与
的大小．
(a>0)对应的变换作用下得到的曲线为x2＋y2＝1.
，B＝
，求矩阵A－1B.
，求矩阵A的特征值．推荐套卷
如图，正三角形ABC的边长为2，D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠，使A、B、C三点重合，构成三棱锥A— DEF ．
(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上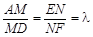， (λ＞O，λ为变量)
①当λ为何值时，MN为异面直线AD与EF的公垂线段? 请证明你的结论②设异面直线MN与AE所成的角为a，异面直线MN与DF所成的角为β，试求a+β 的值
粤公网安备 44130202000953号