如图，某中学甲、乙两班共有25名学生报名参加了一项 测试．这25位学生的考分编成的茎叶图，其中有一个数据因电脑操作员不小心删掉了（这里暂用x来表示），但他清楚地记得两班学生成绩的中位数相同．
（1）求这两个班学生成绩的中位数及x的值；
（2）如果将这些成绩分为“优秀”（得分在175分以上，包括175分）和“过关”，若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛，求这3人中甲班至多有一人入选的概率．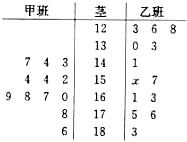
相关试题
的不等式
，其中
是实参数.
时，解上面的不等式.
，上面的不等式均成立，求实数以坐标原点为极点，横轴的正半轴为极轴的极坐标系下，有曲线C：
，过极点的直线
（
且
是参数）交曲线C于两点0，A，令OA的中点为M.
(1)求点M在此极坐标下的轨迹方程（极坐标形式）.
(2)当
时，求M点的直角坐标.
的外接圆的切线
与
的延长线交于点
，
的平分线与
，
＝1.求
长.
。
，讨论
的单调性；
恒有
，求
的取值范围。
是等差数列，
是公比为
的等比数列，
，记
为数列
项和，
是大于
的正整数
，求证：
；
是某一正整数推荐套卷
粤公网安备 44130202000953号