在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是_ ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表法求解).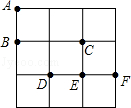
相关知识点
推荐套卷
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是_ ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表法求解).