从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
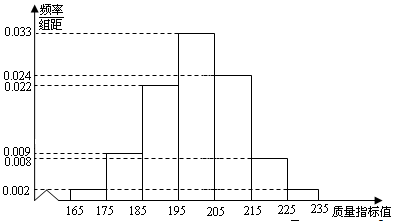
(I)求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标服从正态分布 ,其中近似为样本平均数,
,其中近似为样本平均数, 近似为样本方差.
近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间的产品件数.利用(i)的结果,求.
附:
若 则
则 ,
, 。
。
推荐套卷
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:

(I)求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标服从正态分布 ,其中近似为样本平均数,
,其中近似为样本平均数, 近似为样本方差.
近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间的产品件数.利用(i)的结果,求.
附:
若 则
则 ,
, 。
。