记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
=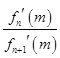 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
推荐套卷
记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
=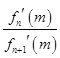 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.