已知函数f(x)＝Asin(2x＋θ)，其中A≠0，θ∈(0，
)．
(1)若函数f(x)的图象过点E(－
，1)，F(
，
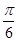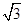)，求函数f(x)的解析式；
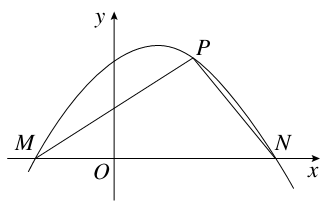
(2)如图，点M，N是函数y＝f(x)的图象在y轴两侧与x轴的两个相邻交点，函数图象上一点P(t，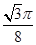
)满足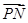
·
＝
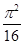，求函数f(x)的最大值．
=
, 
= 
,试用
, 
, 
，
。
；（2）（
－
）－（
－
）。
=
，
=
、
及向量
的坐标；
．
的顶点
、
、
，求顶点
的标．
=（1，
），
=（
，1），
=
=2相关知识点
推荐套卷
已知函数f(x)＝Asin(2x＋θ)，其中A≠0，θ∈(0，)．
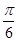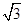(1)若函数f(x)的图象过点E(－，1)，F(，)，求函数f(x)的解析式；
(2)如图，点M，N是函数y＝f(x)的图象在y轴两侧与x轴的两个相邻交点，函数图象上一点P(t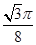，)满足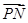·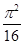＝，求函数f(x)的最大值．
粤公网安备 44130202000953号