（本小题满分12分）
已知抛物线C1:y2=4x的焦点与椭圆C2:
的右焦点F2重合，F1是椭圆的左焦点；
（Ⅰ）在
ABC中，若A(-4,0)，B(0,-3)，点C在抛物线y2=4x上运动，求ABC重心G的轨迹方程；
（Ⅱ）若P是抛物线C1与椭圆C2的一个公共点，且∠PF1F2=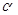
，∠PF2F1=
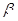,求cos
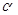
的值及PF1F2的面积。
中，
，公差为
，其前
项和为
，在等比数列
中，
，公比为
，且
，
．
与
；
满足
，求
的前
．
．
取得最大值时，求自变量
的集合；
的值；
的值．
，且
，求：
及
；
的最小值为
，求实数
的值．
，
，且
，
，求角
的值．推荐套卷
（本小题满分12分）
已知抛物线C1:y2=4x的焦点与椭圆C2:的右焦点F2重合，F1是椭圆的左焦点；
（Ⅰ）在ABC中，若A(-4,0)，B(0,-3)，点C在抛物线y2=4x上运动，求ABC重心G的轨迹方程；
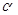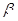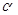
（Ⅱ）若P是抛物线C1与椭圆C2的一个公共点，且∠PF1F2=，∠PF2F1=,求cos的值及PF1F2的面积。
粤公网安备 44130202000953号