地为绿化环境，移栽了银杏树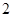
棵，梧桐树
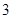棵.它们移栽后的成活率分别
为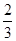
、
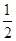，每棵树是否存活互不影响，在移栽的
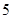棵树中：
（1）求银杏树都成活且梧桐树成活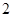棵的概率；
（2）求成活的棵树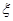
的分布列与期望.
b
求证：
该方程所表示的直线一定过点.
相关知识点
推荐套卷
地为绿化环境，移栽了银杏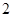树棵，梧桐树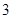棵.它们移栽后的成活率分别
为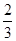、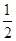，每棵树是否存活互不影响，在移栽的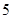棵树中：
（1）求银杏树都成活且梧桐树成活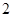棵的概率；
（2）求成活的棵树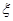的分布列与期望.
粤公网安备 44130202000953号