己知函数
(1)当
时，求函数
的最小值和最大值；
(2)设
ABC的内角A，B，C的对应边分别为a，b，c，且c=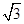
，f(C)=2，若向量m=(1，a)与向量n=(2，b)共线，求a，b的值．
相关试题
在区间
上的最值。(要列表求)
在
处取得极值,并且
在点( 1 , 0 ) 处相切, 求a , b , c的值。
是定义域为R的奇函数；
，试求不等式
的解集；
上的最小值为－2，
a－
的最大值为1时a的值．
的最小正周期为
，
．
，
；
的单调递减区间；
上的图象．
相关知识点
推荐套卷
己知函数
(1)当时，求函数的最小值和最大值；
(2)设ABC的内角A，B，C的对应边分别为a，b，c，且c=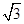，f(C)=2，若向量m=(1，a)与向量n=(2，b)共线，求a，b的值．
粤公网安备 44130202000953号