如图，Rt△ABC中，分别以AB、AC为斜边，向△ABC的内侧作等腰Rt△ABE、Rt△ACD，点M是BC的中点，连接MD、ME.
（1）若AB＝8，AC＝4，求DE的长；
（2）求证：AB－AC＝2DM.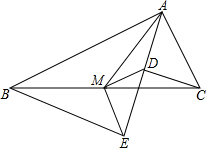
，其中
.
相关知识点
推荐套卷
如图，Rt△ABC中，分别以AB、AC为斜边，向△ABC的内侧作等腰Rt△ABE、Rt△ACD，点M是BC的中点，连接MD、ME.
（1）若AB＝8，AC＝4，求DE的长；
（2）求证：AB－AC＝2DM.
粤公网安备 44130202000953号