一批产品需要进行质量检验,质检部门规定的检验方案是:先从这批产品中任取3件作检验,若3件产品都是合格品,则通过检验;若有2件产品是合格品,则再从这批产品中任取1件作检验,这1件产品是合格品才能通过检验;若少于2件合格品,则不能通过检验,也不再抽检. 假设这批产品的合格率为80%,且各件产品是否为合格品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费为125元,并且所抽取的产品都要检验,记这批产品的检验费为 元,求
元,求 的概率分布及数学期望.
的概率分布及数学期望.
相关知识点
推荐套卷
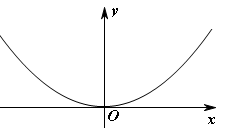
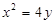 ,过原点作斜率为1的直线交抛物线于第一象限内一点
,过原点作斜率为1的直线交抛物线于第一象限内一点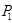 ,又过点
,又过点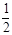 的直线交抛物线于点
的直线交抛物线于点 ,再过
,再过 的直线交抛物线于点
的直线交抛物线于点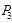 ,
,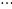 ,如此继续。一般地,过点
,如此继续。一般地,过点 作斜率为
作斜率为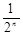 的直线交抛物线于点
的直线交抛物线于点 ,设点
,设点 .
.
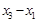 的值;
的值; ,求证:数列
,求证:数列 是等比数列;
是等比数列; 为点列
为点列 的极限点,求点
的极限点,求点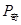 的坐标.
的坐标. .
. 的奇偶性;
的奇偶性; 时,是否存实数
时,是否存实数 ,使
,使 图像的下方,若存在,求
图像的下方,若存在,求
 为抛物线
为抛物线 的焦点,点
的焦点,点 是准线
是准线 上的动点,直线
上的动点,直线 交抛物线
交抛物线 于
于 两点,若点
两点,若点 ,点
,点 为准线
为准线 轴的交点.
轴的交点.
 面积
面积 的取值范围.
的取值范围. 的底面边长
的底面边长 ,若异面直线
,若异面直线 与
与 所成角的大小为
所成角的大小为 ,求正四棱柱
,求正四棱柱

 粤公网安备 44130202000953号
粤公网安备 44130202000953号