在平面直角坐标系xOy中,平面区域W中的点的坐标(x,y)满足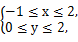
从区域W中随机取点M(x,y).
(1)若x∈Z,y∈Z,求点M位于第一象限的概率.
(2)若x∈R,y∈R,求|OM|≤2的概率.
相关试题
＝(a＋2z)2.
＋2i相关知识点
推荐套卷
在平面直角坐标系xOy中,平面区域W中的点的坐标(x,y)满足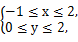从区域W中随机取点M(x,y).
(1)若x∈Z,y∈Z,求点M位于第一象限的概率.
(2)若x∈R,y∈R,求|OM|≤2的概率.
粤公网安备 44130202000953号