已知直线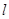
：
(k
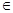R)与圆C:
相交于点A、B, M为弦AB中点．
(Ⅰ) 当k=1时，求弦AB的中点M的坐标及AB弦长；
（Ⅱ）求证：直线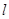与圆C总有两个交点;
（Ⅲ）当k变化时求弦AB的中点M的轨迹方程．
3,求
的值; 
，且
．
在
上的单调性，并给予证明；
. 
的奇偶性；
，集合
．
时，
； (2) 若
，求实数
的取值范围．
和直线
的交点
的坐标，及点
的距离。相关知识点
推荐套卷
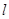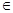已知直线：(kR)与圆C:相交于点A、B, M为弦AB中点．
(Ⅰ) 当k=1时，求弦AB的中点M的坐标及AB弦长；
（Ⅱ）求证：直线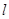与圆C总有两个交点;
（Ⅲ）当k变化时求弦AB的中点M的轨迹方程．
粤公网安备 44130202000953号