设椭圆E：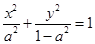
的焦点在x轴上．
(1)若椭圆E的焦距为1，求椭圆E的方程；
(2)设F1、F2分别是椭圆E的左、右焦点，P为椭圆E上第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q.证明：当a变化时，点P在某定直线上．
相关试题
转化为“十进制”数，再把它转化为“八进制”数。
满足如图所示的程序框图．
时输出的结果；
是等比数列；
项和
.
，分别求
，
，
，
万元与销售额
万元之间有如下的对应数据：
，
)推荐套卷
设椭圆E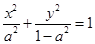：的焦点在x轴上．
(1)若椭圆E的焦距为1，求椭圆E的方程；
(2)设F1、F2分别是椭圆E的左、右焦点，P为椭圆E上第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q.证明：当a变化时，点P在某定直线上．
粤公网安备 44130202000953号