如图所示的两个同心圆盘均被 等分(
等分( 且
且 ),在相重叠的扇形格中依次同时填上
),在相重叠的扇形格中依次同时填上 ,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
(1)求 个不同位置的“旋转和”的和;
个不同位置的“旋转和”的和;
(2)当 为偶数时,求
为偶数时,求 个不同位置的“旋转和”的最小值;
个不同位置的“旋转和”的最小值;
(3)设 ,在如图所示的初始位置将任意
,在如图所示的初始位置将任意 对重叠的扇形格中的两数均改写为0,证明:当
对重叠的扇形格中的两数均改写为0,证明:当 时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
相关知识点
推荐套卷
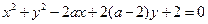 ,其中
,其中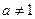 ,且
,且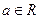 .
. 本小题满分12分)
本小题满分12分)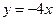 上,且与直线
上,且与直线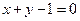 相切于
相切于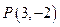
 的圆的方程.
的圆的方程.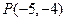 ,且与两坐标轴围成的三角形面积为5,求该直线方程。
,且与两坐标轴围成的三角形面积为5,求该直线方程。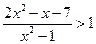
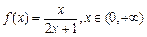 ,数列
,数列 满足
满足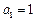 ,
,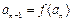 ;数列
;数列 满足
满足 ,
,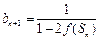 ,其中
,其中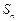 为数列
为数列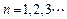
 ,证明
,证明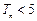 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号