已知曲线 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,设点
,设点 (
( ).
).
(1)指出 ,并求
,并求 与
与 的关系式(
的关系式( );
);
(2)求 (
( )的通项公式,并指出点列
)的通项公式,并指出点列 ,
, ,
, ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由;
(3)令 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
相关知识点
推荐套卷
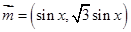 ,
,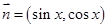 ,设函数
,设函数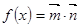 .
. 的解析式,并求
的解析式,并求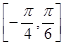 上的最小值;
上的最小值;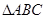 中,
中,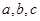 分别是角
分别是角 的对边,
的对边,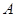 为锐角,若
为锐角,若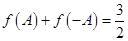 ,
,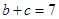 ,
, ,求
,求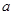 .
.
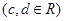 ,其图象为曲线
,其图象为曲线 ,点
,点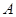 为曲线
为曲线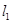 与曲线
与曲线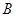 ,在点
,在点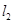 .
. 时,求函数
时,求函数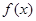 的单调区间;
的单调区间; 时,
时,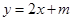 ,求实数
,求实数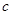 和
和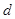 的值;
的值;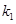 、
、 ,试问:是否存在常数
,试问:是否存在常数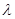 ,使得
,使得 ?若存在,求出
?若存在,求出 的中心在原点,焦点在
的中心在原点,焦点在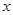 轴上,离心率
轴上,离心率 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线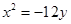 的焦点.
的焦点.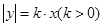 的交点为
的交点为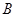 、
、 面积的最大值.
面积的最大值.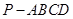 中,
中,  平面
平面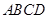 ,
,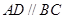 ,
,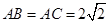 ,
,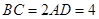 .
. 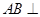 平面
平面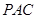 ;
;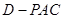 的高.
的高. 
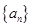 中,点
中,点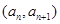
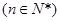 在直线
在直线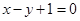 上,且
上,且 .
.  ;
;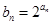 ,数列
,数列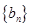 的前
的前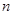 项和为
项和为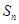 ,
,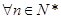 ,
, 成立,求实数
成立,求实数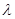 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号