小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.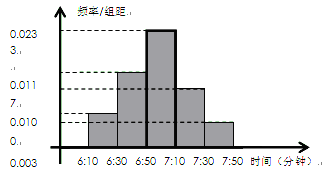
(1)根据图中的数据信息,求出众数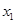 和中位数
和中位数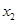 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间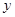 在上午
在上午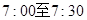 之间,而送报人每天在
之间,而送报人每天在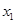 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件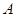 )的概率.
)的概率.
相关知识点
推荐套卷
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数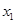 和中位数
和中位数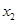 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间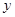 在上午
在上午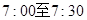 之间,而送报人每天在
之间,而送报人每天在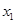 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件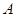 )的概率.
)的概率.