（本小题满分12分）如图，抛物线的顶点O在坐标原点，焦点在y轴的负半轴上，过点M（0，-2）作直线l与抛物线相交于A，B两点，且满足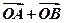
=(-4,-12).
（1）求直
线l和抛物线的方程；
（2）当抛物线上一动点P在点A和B之间运动时，求ΔABP面积的最大
值．
，
为偶函数，求
在区间
上是增函数。
,集合
，
，若
，求实数
的取值范围。
，
， 
。
，
，
。
，则
相关知识点
推荐套卷
（本小题满分12分）如图，抛物线的顶点O在坐标原点，焦点在y轴的负半轴上，过点M（0，-2）作直线l与抛物线相交于A，B两点，且满足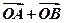=(-4,-12).
（1）求直线l和抛物线的方程；
（2）当抛物线上一动点P在点A和B之间运动时，求ΔABP面积的最大值．
粤公网安备 44130202000953号