如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．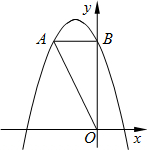
（1）求△OAB的面积；
（2）若抛物线y=-x2-2x+c经过点A．
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．
相关试题
＝1－
， 
＝
， 
＝
，
＝
＝0 ,试求：
＋
＋
＋ …… ＋
的值．相关知识点
推荐套卷
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．
（1）求△OAB的面积；
（2）若抛物线y=-x2-2x+c经过点A．
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．
粤公网安备 44130202000953号