(·黑龙江哈尔滨)(本题10分)
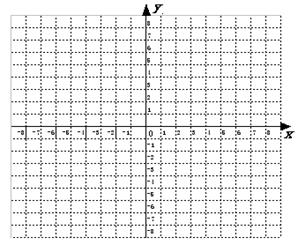
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+1(k≠0)与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2-(6a-2)x+b (a≠0)与直线AC交于另一点B,点B坐标为(4,3).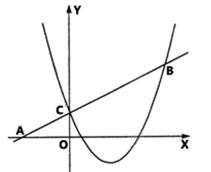
(1)求a的值;
(2)点p是射线CB上的一个动点,过点P在作PQ⊥x轴,垂足为点Q,在x轴上点Q的右侧取点M,使MQ=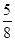 ,在QP的延长线上取点N,连接PM,AN,已知tan∠NAQ-tan∠MPQ=
,在QP的延长线上取点N,连接PM,AN,已知tan∠NAQ-tan∠MPQ=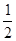 ,求线段PN的长;
,求线段PN的长;
(3)在(2)的条件下,过点C作CD⊥AB,使点D在直线AB 下方,且CD=AC,连接PD,NC,当以PN,PD,NC的长为三边长构成的三角形面积是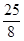 时,在y轴左侧的抛物线上是否存在点E,连接NE,PE,使得ΔENP与以PN、PD、NC的长为三边长的三角形全等?若存在,求出点E坐标;若不存在,请说明理由.
时,在y轴左侧的抛物线上是否存在点E,连接NE,PE,使得ΔENP与以PN、PD、NC的长为三边长的三角形全等?若存在,求出点E坐标;若不存在,请说明理由.
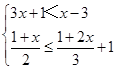 并写出它的整数解
并写出它的整数解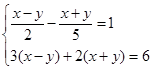
 粤公网安备 44130202000953号
粤公网安备 44130202000953号