一个三角形数表按如下方式构成(如图:其中项数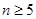 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: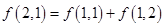 ;
;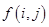 为数表中第
为数表中第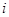 行的第
行的第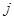 个数.
个数.
求第2行和第3行的通项公式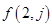 和
和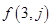 ;
;
证明:数表中除最后2行外每一行的数都依次成等差数列,并求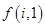 关于
关于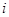 (
(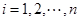 )的表达式;
)的表达式;
(3)若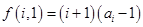 ,
, ,试求一个等比数列
,试求一个等比数列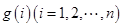 ,使得
,使得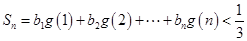 ,且对于任意的
,且对于任意的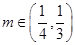 ,均存在实数
,均存在实数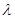 ,当
,当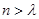 时,都有
时,都有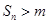 .
.
相关知识点
推荐套卷
一个三角形数表按如下方式构成(如图:其中项数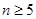 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: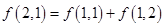 ;
;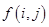 为数表中第
为数表中第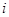 行的第
行的第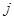 个数.
个数.
求第2行和第3行的通项公式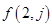 和
和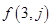 ;
;
证明:数表中除最后2行外每一行的数都依次成等差数列,并求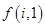 关于
关于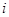 (
(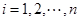 )的表达式;
)的表达式;
(3)若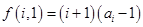 ,
, ,试求一个等比数列
,试求一个等比数列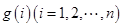 ,使得
,使得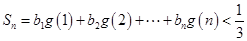 ,且对于任意的
,且对于任意的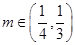 ,均存在实数
,均存在实数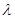 ,当
,当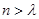 时,都有
时,都有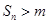 .
.