甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束，除第五局甲队获胜的概率是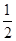
外，其余每局比赛甲队获胜的概率都是
，假设各局比赛结果相互独立．
(1)分别求甲队以3∶0，3∶1，3∶2胜利的概率；
(2)若比赛结果为3∶0或3∶1，则胜利方得3分，对方得0分；若比赛结果为3∶2，则胜利方得2分、对方得1分．求乙队得分X的分布列．
相关试题
，
，
，
，求
的
，
，
，
．（Ⅰ）当
时，求
值的集合； （Ⅱ）求
的最大值．
与
互相垂直，其中
．
和
的值；（2）若
，求
的值．
值依
；
，…，
，….
和
的通项公式；
,求数列
的前
项和
，
其中
.推荐套卷
甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束，除第五局甲队获胜的概率是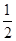外，其余每局比赛甲队获胜的概率都是，假设各局比赛结果相互独立．
(1)分别求甲队以3∶0，3∶1，3∶2胜利的概率；
(2)若比赛结果为3∶0或3∶1，则胜利方得3分，对方得0分；若比赛结果为3∶2，则胜利方得2分、对方得1分．求乙队得分X的分布列．
粤公网安备 44130202000953号