已知抛物线C：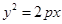
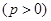，点A、B在抛物线C上.
（1）若直线AB过点M（2p，0），且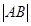
=4p，求过A，B，O（O为坐标原点）三点的圆的方程；
（2）设直线OA、OB的倾斜角分别为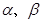
，且
，问直线AB是否会过某一定点？若是，求出这一定点的坐标，若不是，请说明理由.
相关试题
的定义域为集合
，函数
的定义域为集合
．
和
；（2）若
，求实数
的取值范围．
，若
中元素至多只有一个，求
的取值范围.
.
为何实数
总是为增函数；
的顶点坐标为
，且
，
∈
，
的图象恒在
的图象上方，
的取值范围，
上单调，求实数
的取值范围.
是定义在
上的增函数，且
的值；（2）解不等式：
；
，解不等式
相关知识点
推荐套卷
已知抛物线C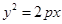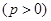：，点A、B在抛物线C上.
（1）若直线AB过点M（2p，0），且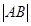=4p，求过A，B，O（O为坐标原点）三点的圆的方程；
（2）设直线OA、OB的倾斜角分别为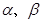，且，问直线AB是否会过某一定点？若是，求出这一定点的坐标，若不是，请说明理由.
粤公网安备 44130202000953号