已知动点 到直线
到直线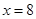 的距离是它到点
的距离是它到点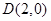 的距离的2倍.记
的距离的2倍.记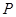 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)求定圆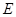 的方程,使圆
的方程,使圆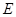 与以
与以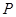 为圆心,
为圆心,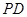 为半径的圆内切.
为半径的圆内切.
(3)已知定点 ,是否存在斜率为1的直线
,是否存在斜率为1的直线 与曲线
与曲线 交于不同的两点
交于不同的两点 ,使得
,使得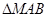 是以
是以 为底边为等腰三角形,若存在,求出
为底边为等腰三角形,若存在,求出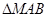 的面积,若不存在,说明理由.
的面积,若不存在,说明理由.
推荐套卷
已知动点 到直线
到直线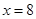 的距离是它到点
的距离是它到点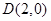 的距离的2倍.记
的距离的2倍.记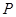 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)求定圆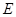 的方程,使圆
的方程,使圆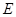 与以
与以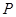 为圆心,
为圆心,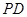 为半径的圆内切.
为半径的圆内切.
(3)已知定点 ,是否存在斜率为1的直线
,是否存在斜率为1的直线 与曲线
与曲线 交于不同的两点
交于不同的两点 ,使得
,使得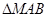 是以
是以 为底边为等腰三角形,若存在,求出
为底边为等腰三角形,若存在,求出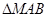 的面积,若不存在,说明理由.
的面积,若不存在,说明理由.