在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点) :
: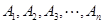 与
与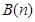 :
: ,其中
,其中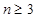 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段 ,其中
,其中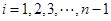 ,则称
,则称 与
与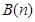 互为正交点列.
互为正交点列.
(1)试判断 :
: 与
与 :
: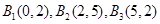 是否互为正交点列,并说明理由;
是否互为正交点列,并说明理由;
(2)求证: :
: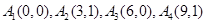 不存在正交点列
不存在正交点列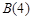 ;
;
(3)是否存在无正交点列 的有序整数点列
的有序整数点列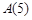 ?并证明你的结论.
?并证明你的结论.
相关知识点
推荐套卷
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点) :
: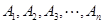 与
与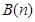 :
: ,其中
,其中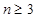 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段 ,其中
,其中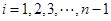 ,则称
,则称 与
与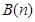 互为正交点列.
互为正交点列.
(1)试判断 :
: 与
与 :
: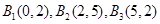 是否互为正交点列,并说明理由;
是否互为正交点列,并说明理由;
(2)求证: :
: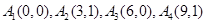 不存在正交点列
不存在正交点列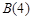 ;
;
(3)是否存在无正交点列 的有序整数点列
的有序整数点列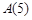 ?并证明你的结论.
?并证明你的结论.