高中数学柯西不等式与排序不等式试题

若，，向量与的夹角为，则向量在上的投影为 .

设是外接圆的圆心，，且，，，则.

在中，角所对的边分别为。已知，.
(1)若，求的面积； (2)求的值.

在中，角所对的边分别为。已知，.
(1)若，求的面积； (2)求的值.

设分别是的斜边上的两个三等分点，已知，则．

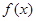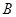
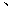
若函数的图像与轴交于点，过点的直线与函数的图像交于两点，则（）

A．－32

B．－16

C．16

D．32

给出下列四个命题：
① 因为，所以；
② 由两边同除，可得；
③ 数列1，4，7，10，…，的一个通项公式是；
④ 演绎推理是由一般到特殊的推理，类比推理是由特殊到特殊的推理．
其中正确命题的个数有（）

A．1个

B．2个

C．3个

D．4个

给出下列结论：①若，，则； ②若，则；
③；④为非零不共线，若；
⑤非零不共线，则与垂直
其中正确的为（）

A．②③

B．①②④

C．④⑤

D．③④

若干个能唯一确定一个数列的量称为该数列的“基本量”.设是公比为的无穷等比数列，下列的四组量中，一定能成为该数列“基本量”的是第组；
①；②；③；④.

给出下面四个命题，不正确的是：．
①若向量、满足，且与的夹角为，则在上的投影等于；
②若等比数列的前项和为，则、、也成等比数列；
③常数列既是等差数列，又是等比数列；
④若向量与共线，则存在唯一实数，使得成立。
⑤在正项等比数列中，若，则

在平面直角坐标系中，对于任意相邻三点都不共线的有序整点列（整点即横纵坐标都是整数的点）：与：，其中，若同时满足：①两点列的起点和终点分别相同；②线段，其中，则称与互为正交点列.
（1）试判断：与：是否互为正交点列，并说明理由；
（2）求证：：不存在正交点列；
（3）是否存在无正交点列的有序整数点列？并证明你的结论.

①设a，b是两个非零向量，若|a+b|=|a-b|，则a·b=0
②若③在△ABC中，若，则△ABC是等腰三角形④在中，，边长a,c分别为a=4,c=，则只有一解。
上面说法中正确的是

设为平面直角坐标系内的点集，若对于任意，存在，使得，则称点集满足性质. 给出下列四个点集：
1；
2；
3；
④
其中所有满足性质的点集的序号是______．

是边延长线上一点，记. 若关于的方程
在上恰有两解，则实数的取值范围是（）

A．	B．或
C．	D．或

已知向量a＝(m，n)，b＝(p，q)，定义a⊗b＝mn－pq.给出下列四个结论：①a⊗a＝0；②a⊗b＝b⊗a；③(a＋b)⊗a＝a⊗a＋b⊗a；④(a⊗b)²＋(a·b)²＝(m²＋q²)·(n²＋p²)．
其中正确的结论是________．(写出所有正确结论的序号)