如图，在四棱锥PABCD中，PD⊥底面ABCD，AD⊥AB，CD∥AB，AB＝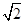
AD＝2，CD＝3，直线PA与底面ABCD所成角为60°，点M、N分别是PA、PB的中点．求证：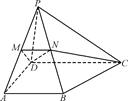
(1)MN∥平面PCD；
(2)四边形MNCD是直角梯形；
(3)DN⊥平面PCB.
相关试题
上随机取两个数m、n，求关于x的一元二次方程
有实根的概率．
，得到黑球或黄球的概率是
，得到黄球或绿球的概率也是推荐套卷
如图，在四棱锥PABCD中，PD⊥底面ABCD，AD⊥AB，CD∥AB，AB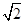＝AD＝2，CD＝3，直线PA与底面ABCD所成角为60°，点M、N分别是PA、PB的中点．求证：
(1)MN∥平面PCD；
(2)四边形MNCD是直角梯形；
(3)DN⊥平面PCB.
粤公网安备 44130202000953号