如图，四边形ABCD为正方形，在四边形ADPQ中，PD∥QA.又QA⊥平面ABCD，QA＝AB＝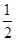
PD.
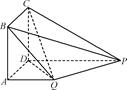
(1)证明：PQ⊥平面DCQ；
(2)CP上是否存在一点R，使QR∥平面ABCD，若存在，请求出R的位置，若不存在，请说明理由．
求
的值.
时的值域； 
中，已知圆
和圆
.
经过点
（2，-1）和圆
的圆心，求直线
的中点，求直线
过点
，且被圆
截得的弦长为
，求直线
的方程.
，求
. 
，求
的值.推荐套卷
如图，四边形ABCD为正方形，在四边形ADPQ中，PD∥QA.又QA⊥平面ABCD，QA＝AB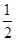＝PD.
(1)证明：PQ⊥平面DCQ；
(2)CP上是否存在一点R，使QR∥平面ABCD，若存在，请求出R的位置，若不存在，请说明理由．
粤公网安备 44130202000953号