已知
是非零实数,抛物线
的焦点
在直线
上.
(I)若
,求抛物线
的方程
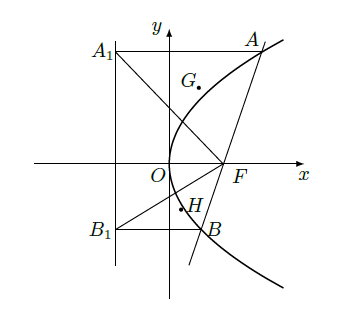
(II)设直线
与抛物线
交于
、
,
,的重心分别为
.求证:对任意非零实数
,抛物线
的准线与
轴的焦点在以线段
为直径的圆外.
相关知识点
推荐套卷
已知
是非零实数,抛物线
的焦点
在直线
上.
(I)若
,求抛物线
的方程
(II)设直线
与抛物线
交于
、
,
,的重心分别为
.求证:对任意非零实数
,抛物线
的准线与
轴的焦点在以线段
为直径的圆外.
