如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得，已知FA⊥平面ABC，AB＝2，BD＝1，AF＝2， CE＝3，O为AB的中点．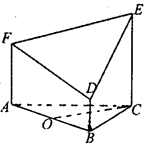
（1）求证：OC⊥DF；
（2）求平面DEF与平面ABC相交所成锐二面角的大小；
（3）求多面体ABC—FDE的体积V．
相关试题
终边上一点P（－4，3），求
的值
；
处的切线方程；
的取值范围．
到它的两焦点F1、F2的距离之和为4，A、B分别是它的左顶点和上顶点..
推荐套卷
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得，已知FA⊥平面ABC，AB＝2，BD＝1，AF＝2， CE＝3，O为AB的中点．
（1）求证：OC⊥DF；
（2）求平面DEF与平面ABC相交所成锐二面角的大小；
（3）求多面体ABC—FDE的体积V．
粤公网安备 44130202000953号