设不等式组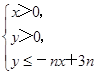
所表示的平面区域为Dn，记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{an}的通项公式；
(2)记数列{an}的前n项和为Sn，且Tn＝
.若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．
，B＝{x|x2－2x－m<0}，相关知识点
推荐套卷
设不等式组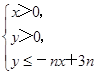所表示的平面区域为Dn，记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{an}的通项公式；
(2)记数列{an}的前n项和为Sn，且Tn＝.若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．
粤公网安备 44130202000953号