甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为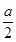 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多 a万元.
a万元.
(1)设甲、乙两超市第n年的销售额分别为an、bn,求an、bn的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
相关知识点
推荐套卷
甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为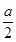 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多 a万元.
a万元.
(1)设甲、乙两超市第n年的销售额分别为an、bn,求an、bn的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?