已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)=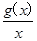 .
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.
相关知识点
推荐套卷
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)=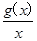 .
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.