已知椭圆M: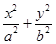 =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4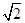 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.
推荐套卷
已知椭圆M: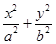 =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4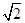 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.