(本题12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面 (编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用
(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用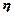 表示更换的面数,用
表示更换的面数,用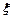 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出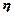 的分布列,求
的分布列,求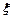 的数学期望。
的数学期望。
推荐套卷
(本题12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面 (编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用
(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用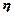 表示更换的面数,用
表示更换的面数,用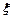 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出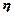 的分布列,求
的分布列,求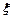 的数学期望。
的数学期望。