已知椭圆C: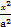
+
=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为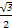
,求椭圆的标准方程.
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)过原点O任意作两条互相垂直的直线与椭圆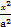+=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
相关试题
），
.
，求角
的值； (2)若
，求
.
，函数
，当
时，
．
的值；（2）求
是同一平面内的三个向量，其中
.
平行的单位向量
的坐标；
，且
与
垂直，求
的夹角
.
的终边经过点
，求下列各式的值：
;（2）
.
的解集为A，不等式
的解集为B，（1）求A
，求a的取值范围推荐套卷
已知椭圆C: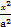+=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为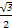,求椭圆的标准方程.
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)过原点O任意作两条互相垂直的直线与椭圆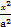+=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
粤公网安备 44130202000953号