(本小题满分12分)
某校在招收体育特长生时,须对报名学生进行三个项目的测试.规定三项都合格者才能录取.假定每项测试相互独立,学生 各项测试合格的概率组成一个公差为
各项测试合格的概率组成一个公差为 的等差数列,且第一项测试不合格的概率超过
的等差数列,且第一项测试不合格的概率超过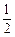 ,第一项测试不合格但第二项测试合格的概率为
,第一项测试不合格但第二项测试合格的概率为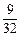 .
.
(Ⅰ)求学生 被录取的概率;
被录取的概率;
(Ⅱ)求学生 测试合格的项数
测试合格的项数 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
(本小题满分12分)
某校在招收体育特长生时,须对报名学生进行三个项目的测试.规定三项都合格者才能录取.假定每项测试相互独立,学生 各项测试合格的概率组成一个公差为
各项测试合格的概率组成一个公差为 的等差数列,且第一项测试不合格的概率超过
的等差数列,且第一项测试不合格的概率超过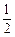 ,第一项测试不合格但第二项测试合格的概率为
,第一项测试不合格但第二项测试合格的概率为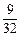 .
.
(Ⅰ)求学生 被录取的概率;
被录取的概率;
(Ⅱ)求学生 测试合格的项数
测试合格的项数 的分布列和数学期望.
的分布列和数学期望.