(本小题满分12分)
| 动作 |
K动作 |
D动作 |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
0.75 |
0.25 |
0.75 |
0.25 |
表1 甲系列
| 动作 |
K动作 |
D动作 |
||
| 得分 |
90 |
5 0 0 |
20 |
0 |
| 概率 |
0.9 |
0 .1 .1 |
0.9 |
0.1 |
表2 乙系列
推荐套卷
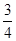
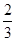
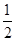
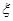 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求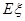 .
.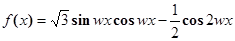 ,
,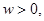
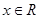 且函数
且函数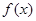 的最小正周期为
的最小正周期为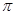 .
.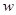 的值和函数
的值和函数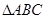 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是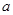 、
、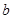 、
、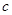 ,又
,又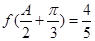 ,
,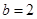 ,
,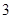 ,求边长
,求边长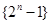 的前
的前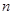 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取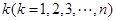 个数,其所有可能的
个数,其所有可能的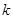 个数的乘积的和为
个数的乘积的和为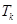 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,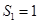 ;当
;当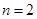 时,
时, ,
, ,
,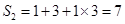 .
. ;
;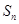 ,并用数学归纳法证明.
,并用数学归纳法证明.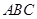 的底边
的底边 ,点
,点 在线段
在线段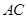 上,
上,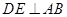 于
于 ,现将
,现将 沿
沿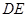 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
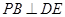 ;
;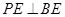 ,直线
,直线 与平面
与平面 所成的角为
所成的角为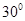 ,求
,求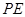 长.
长.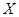 为选取女生的人数,求X的分布列及数学期望.
为选取女生的人数,求X的分布列及数学期望. 粤公网安备 44130202000953号
粤公网安备 44130202000953号