在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系．圆C1，直线C2的极坐标方程分别为ρ＝4sin θ，ρcos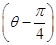 
＝2
.
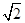(1)求C1与C2交点的极坐标；
(2)设P为C1的圆心，Q为C1与C2交点连线的中点．已知直线PQ的参数方程为
(t∈R为参数)，求a，b的值．
相关试题
的最小正周期和图象的对称轴方程
上的值域
)2+lg
·lg5+
;
=
,求
的值
，（
，且
）．
的定义域；
的取值范围．
，
，
，其中
． 
时，求
值的集合； 
的最大值．
，
（其中
）的周期为π，且图象上一个最低点为
。
的解析式；
时，求相关知识点
推荐套卷
在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系．圆C1，直线C2的极坐标方程分别为ρ＝4sin θ，ρcos 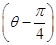＝2.
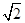(1)求C1与C2交点的极坐标；
(2)设P为C1的圆心，Q为C1与C2交点连线的中点．已知直线PQ的参数方程为 (t∈R为参数)，求a，b的值．
粤公网安备 44130202000953号