已知 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为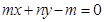 (
( 为常数且
为常数且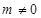 ).
).
(1)求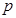 的值;
的值;
(2)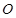 为抛物线的顶点,
为抛物线的顶点, ,
, ,
,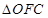 的面积分别记为
的面积分别记为 ,
, ,
, ,求证:
,求证: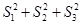 为定值.
为定值.
相关知识点
推荐套卷
已知 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为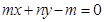 (
( 为常数且
为常数且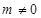 ).
).
(1)求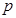 的值;
的值;
(2)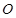 为抛物线的顶点,
为抛物线的顶点, ,
, ,
,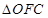 的面积分别记为
的面积分别记为 ,
, ,
, ,求证:
,求证: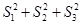 为定值.
为定值.