已知数列{an}是等差数列,a2=6,a5=12,数列{bn}的前n项和是Sn,且Sn+
bn=1.
(1)求数列{an}的通项公式.
(2)求证:数列{bn}是等比数列.
(3)记cn=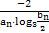
,{cn}的前n项和为Tn,若Tn<
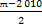对一切n∈N*都成立,求最小正整数m.
相关试题
，
与
共线．
的值；
在区间上
的最大值和最小值．
，其中
为实常数．
的奇偶性；
，使不等式
恒成立，求
的焦点
的直线交
于
两点，且
的值；
是
的垂直平分线交
轴于点
，求
的面积的最小值．
满足下列条件：
，
的通项公式；
与
的大小．
中，
，
，
，
。
平面
；
为
上的一点．若直线
与平面
，求
的长．相关知识点
推荐套卷
已知数列{an}是等差数列,a2=6,a5=12,数列{bn}的前n项和是Sn,且Sn+bn=1.
(1)求数列{an}的通项公式.
(2)求证:数列{bn}是等比数列.
(3)记cn=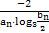,{cn}的前n项和为Tn,若Tn<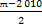对一切n∈N*都成立,求最小正整数m.
粤公网安备 44130202000953号